Problem Definition
The three-dimensional steel truss structure shown below is composed of 264 members and 88 nodes (including 8 supported nodes). Sizing optimization of this truss is considered. The topology of the truss (i.e., the way that the nodes are connected to each other) is assumed to be fixed and unchangeable. The structure is designed under three independent load cases, where the loads are applied at all unsupported nodes of the truss in the following cases: (i) horizontal loads of 11 kN applied in the positive x-direction, (ii) horizontal loads of 11 kN applied in the positive y-direction, (iii) vertical loads of 14 kN applied in the negative z-direction. The material density, elastic modulus, and yield stress of the truss material are 7.85 ton/m3, 200 GPa and 248.2 MPa, respectively. The structure is designed in accordance with the regulations of AISC-LRFD 1994. To this end, each member is checked considering the limit states of tensile yielding and compressive buckling. A simple MATLAB function for the structural analysis and design of this particular truss is provided below.
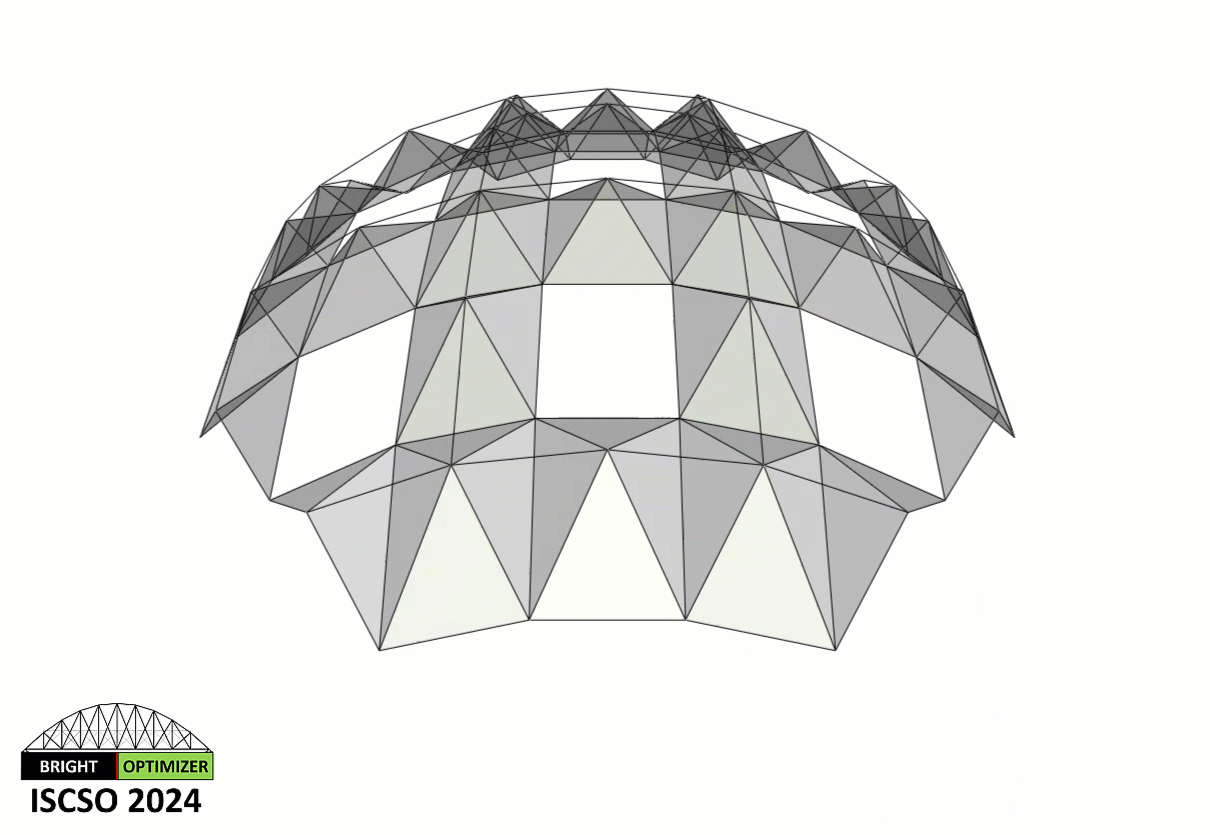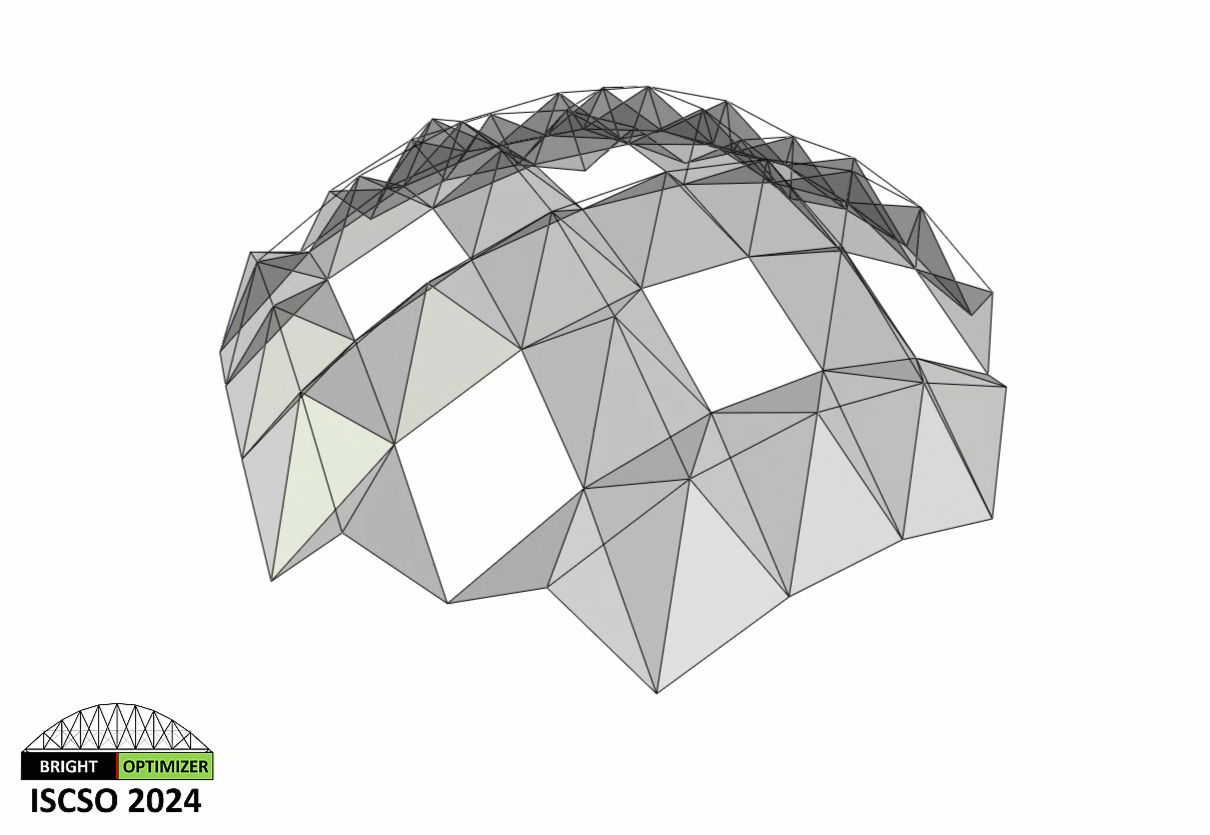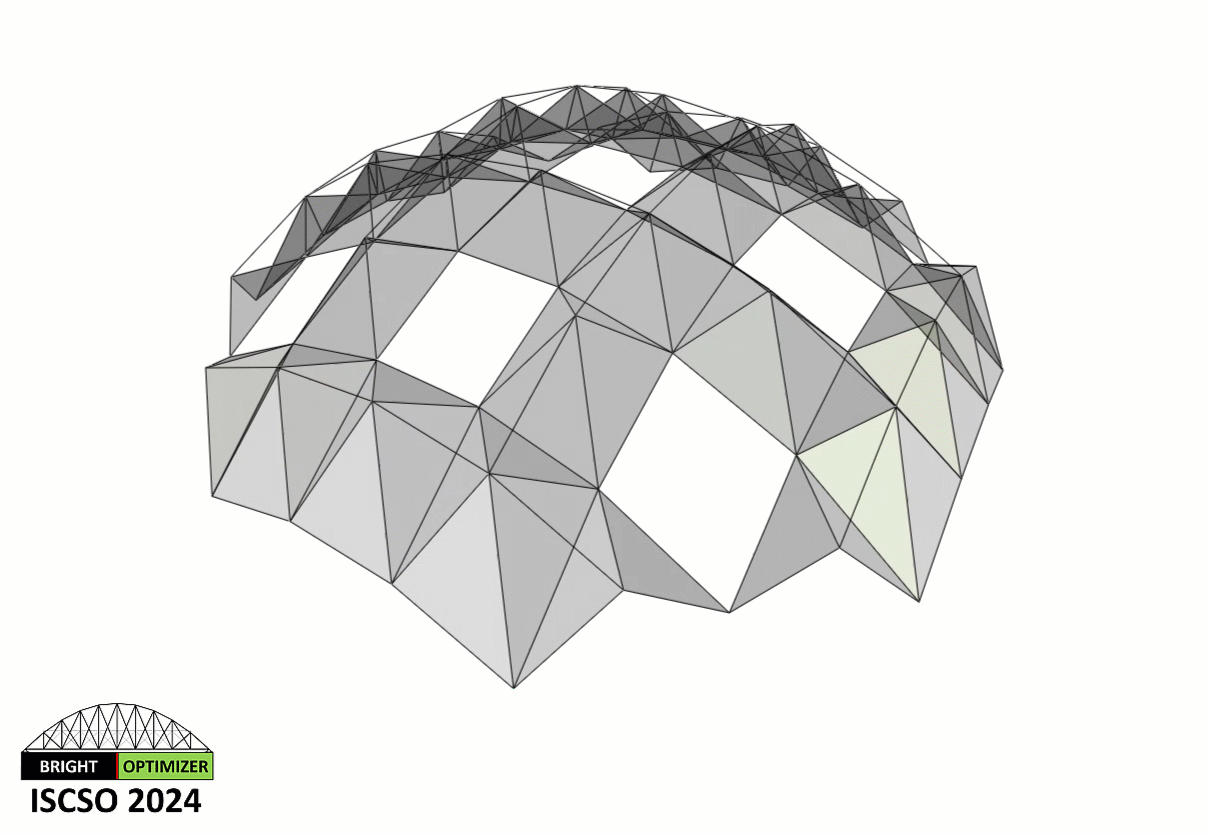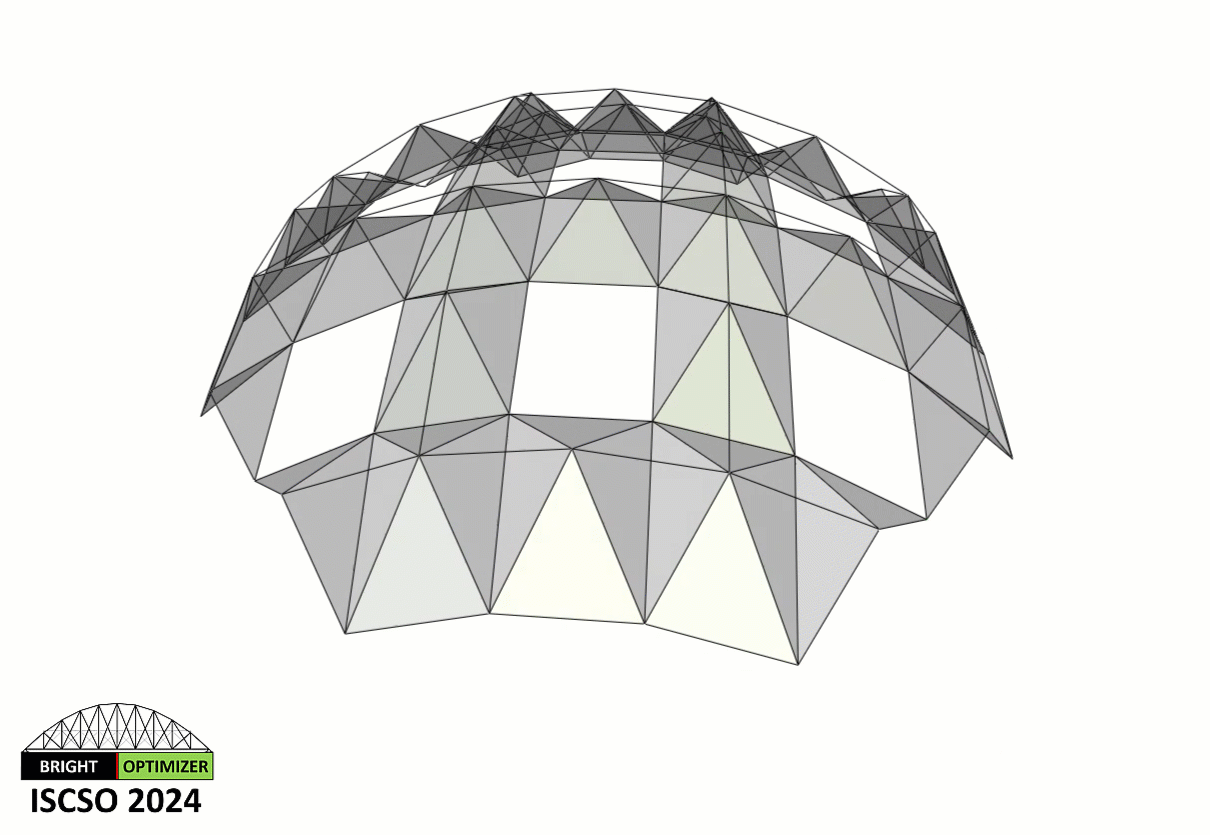
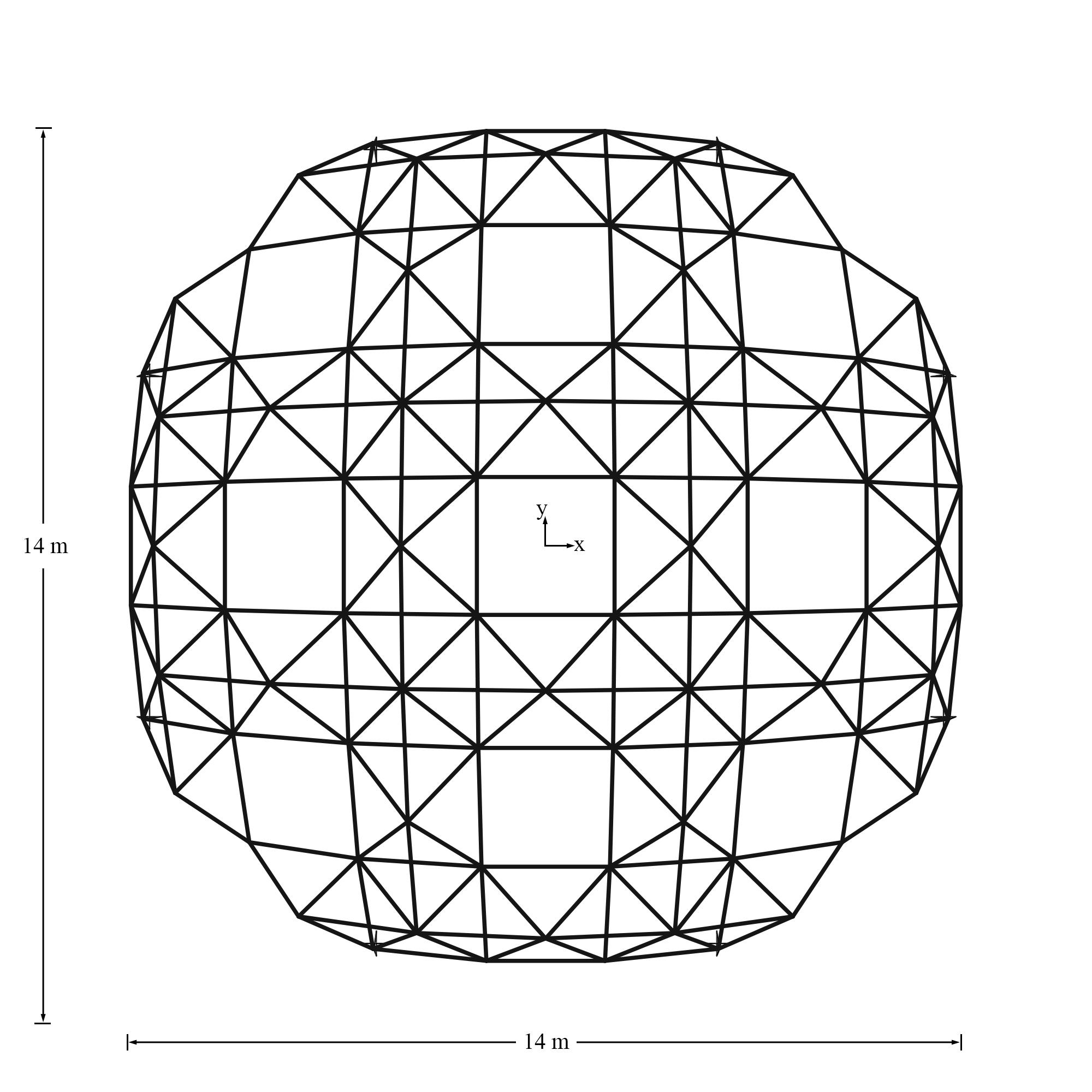
This problem includes 264 sizing variables which represent the cross-sections of the truss members. The following should be satisfied:
- Find the sizing variables (S1 to S264) which minimize the following two objectives:
- Obj_Func_1: Weight of the structure (F1)
- Obj_Func_2: Maximum nodal displacement (F2)
according to the given constraints. However, the maximum number of objective function evaluations that you are allowed to perform, using the given MATLAB function, is 1,000,000 times. In other words, you are only allowed to call the given MATLAB function 1,000,000 times (maximum) during your optimization process. Note that, structural analysis and design shall be performed using the given MATLAB function only.
- You can use any optimization technique. Further, you may propose a new optimization algorithm or a hybrid form of previously proposed algorithms. However, using commercial optimization software is not allowed and the participants must prepare their own original codes.
- The optimization process shall always start from a random point in the search space. In other words, the initial 264 design variables of your optimization procedure must be selected randomly.
- The sizing variables (S1 to S264) can only take integer values ranging from 1 through 37 (i.e. 1 ≤ Si ≤ 37). Each sizing variable represents a section ID from the following database of 37 pipe sections.
- The final Pareto front shall be composed of only non-dominated feasible solutions (i.e., no constraint violation is allowed in the reported set of Pareto-optimal solutions). The amount of constraint violation associated with each candidate design is also reported by the structural analysis and design MATLAB function, given below.
- Grouping of the design variables is not allowed neither at the beginning of the optimization process nor in the course of optimization.
- For the sake of conformity, please solve the problem in the given units.
- Submit a compressed folder (a single archive file, *.rar or *.zip) that contains the following three files through the submission system before the deadline:
- 1- MATLAB code of the optimization algorithm
- 2- The final set of feasible Pareto-optimal solutions. This file must contain the optimum values of decision variables and corresponding objectives and constrain violations (a single MATLAB data file , e.g., “Results.mat”). In this MATLAB data file, the results shall be tabulated in the following order:
| S1 | S2 | … | S263 | S264 | F1 (Obj Func 1) | F2 (Obj Func 2) | C (Const Vio Stress) | |
| Solution 1 | ||||||||
| Solution 2 | ||||||||
| Solution 3 | ||||||||
| ⋮ |
- 3- A brief description of your optimization approach together with the hypervolume (HV) of the final feasible Pareto-optimal solutions with respect to the specified reference point (a single PDF file). You should calculate the HV with respect to the following procedure.
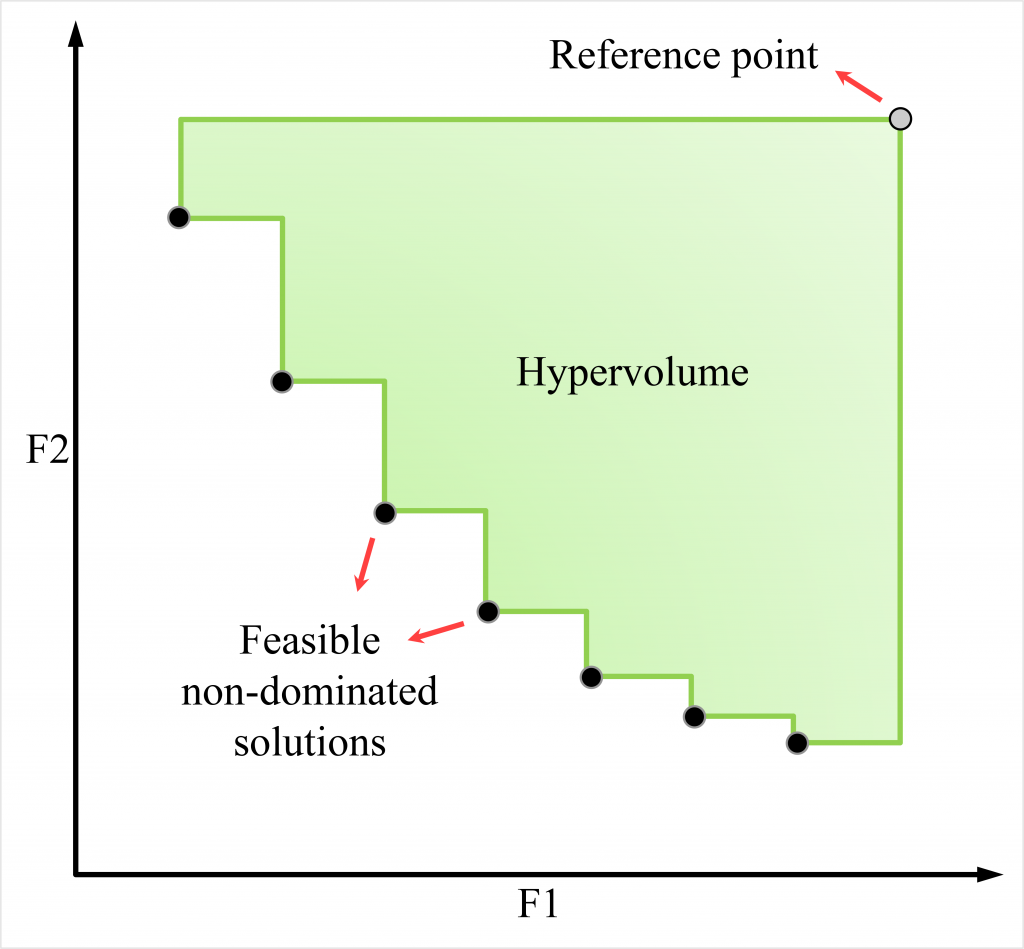
Hypervolume and Reference Point
The hypervolume (HV) shall be calculated by determining the area between the feasible non-dominated solutions on the final Pareto front and the predetermined reference point as shown below. The reference point should be taken as:
Reference point = (F1, F2) = (57319, 10.5)
It should be noted that to calculate the HV of the final feasible Pareto front, the non-dominated solutions that have F2 values greater than 10.5 (if any), should be excluded from the calculations.
Structural Analysis and Design Function
A simple MATLAB function is provided for the structural analysis and design of the given truss system. The file can be downloaded from here. Please extract the zip file to get the MO_ISCSO_2024.p MATLAB function. You can readily use this function anywhere in your optimization code using the following command:
[Obj_Func_1, Obj_Func_2, Const_Vio_Stress]=MO_ISCSO_2024(Sections, Flag)
The terms inside the parentheses on the right-hand side of the function represent the input variables which you should provide to the function:
- “Sections” is a row vector (size 1×264) which contains the sizing variables S1 to S264.
- “Flag” is either 0 or 1. The value of zero indicates that no graphical output is requested from the function. This option is often used for computational efficiency during the optimization process where graphical output is not required. On the other hand, if Flag is set to 1, the function will plot the undeformed geometry of the proposed truss structure. In addition, the members that violate the stress constraints are colored in red. This is further discussed below.
The terms inside the brackets on the left-hand side of the function represent the output variables which are calculated by the function and reported to your MATLAB Workspace:
- “Obj_Func_1” is the weight of the structure (F1)
- “Obj_Func_2” is the maximum nodal displacement of the structure (F2)
- “Const_Vio_Stress” is the amount of constraint violation based on the stress constraints (C). If a value of zero is reported by the function it means that all of the truss members have satisfied the stress requirements. Any value larger than zero indicates that one or more truss members have not satisfied the design regulations of AISC-LRFD 1994.
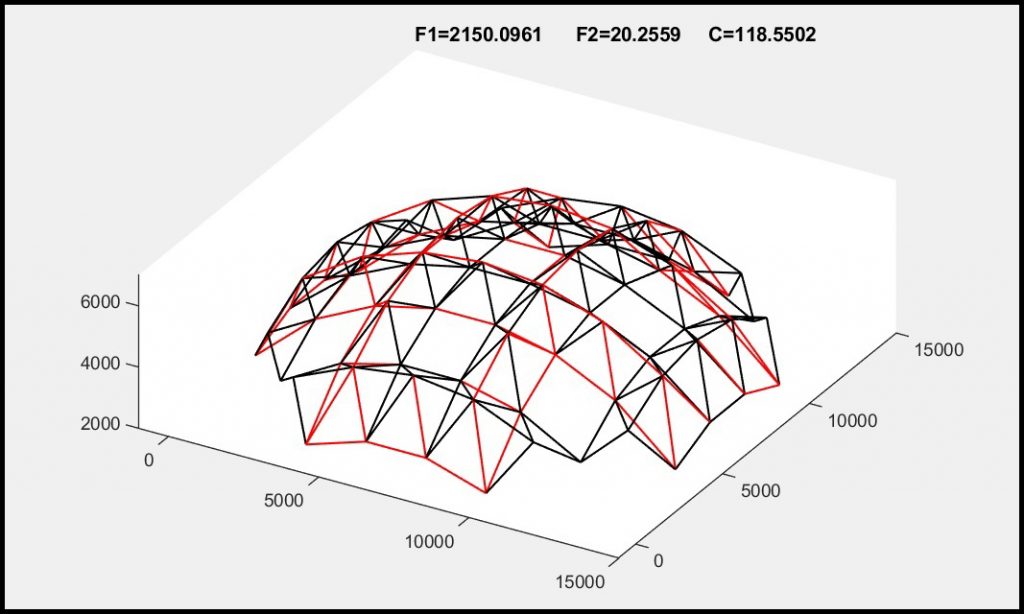
The utilization of the given MATLAB function is further discussed through an example. Assume that the section ID for all the members of a proposed truss structure is equal to 8. To evaluate this structure, a row vector is first defined:
Sections = [8, 8, 8,…, 8] 1×264
Afterwards, the MO_ISCSO_2024 function should be executed. Here, the value of Flag is set equal to 1, assuming that the graphical output is requested by the user. If the graphical output is not required, the Flag (last term inside the parentheses) should be set equal to 0 in the following command:
[Obj_Func_1, Obj_Func_2, Const_Vio_Stress]=MO_ISCSO_2024(Sections, 1)
By executing the above command, three output variables (“Obj_Func_1”, “Obj_Func_2”, and “Const_Vio_Stress”) will appear in your MATLAB Workspace and the following figure will be plotted on your screen which can be moved and resized if needed:
The members that are colored in red represent the members that violate the stress constraints. At the top of the figure, the value of the first objective function (F1), the value of the second objective function (F2), and the total amount of constraint violation (C) are displayed.